CG-Assignment-3

Question-1

a)

Given the basis function of Bezier curve and BSpline curve on page 63 of PPT

please derive the conversion matrix to convert the control points of Bezier curve to the control points of BSpline curve.

Matrix Formulation of the Curves

For a cubic curve, the position vector $Q(t)$ can be written in the general form:

$$Q(t)=\mathbf{G}\mathbf{B}\mathbf{T}(t)$$

where:

• $\mathbf{G}$ = vector of geometry/control points (either Bézier or B-Spline points)
• $\mathbf{B}$ = basis matrix (either $B_{Bezier}$ or $B_{B-Spline}$)
• $\mathbf{T}(t)={\left[\begin{array}{cccc}{t}^3& t^2& t& 1\end{array}\right]}^T$

Given Basis Matrices

Bézier basis:

$${\mathbf{B}}_{Bezier}=\left(\begin{array}{cccc}-1& 3& -3& 1\\ 3& -6& 3& 0\\ -3& 3& 0& 0\\ 1& 0& 0& 0\end{array}\right)$$

B-Spline basis (uniform, cubic):

$${\mathbf{B}}_{B\text{-}Spline}=\frac{1}{6}\left(\begin{array}{cccc}-1& 3& -3& 1\\ 3& -6& 0& 4\\ -3& 3& 3& 1\\ 1& 0& 0& 0\end{array}\right)$$

Relating the Parametric Curves

Both parameterizations describe the same cubic curve $Q(t)$, so:

$${\mathbf{G}}_{Bezier}{\mathbf{B}}_{Bezier}\mathbf{T}(t)={\mathbf{G}}_{BSpline}{\mathbf{B}}_{BSpline}\mathbf{T}(t)$$

Since this should be true for all $t$, and $\mathbf{T}(t)$ is arbitrary, we must have:

$${\mathbf{G}}_{Bezier}{\mathbf{B}}_{Bezier}={\mathbf{G}}_{BSpline}{\mathbf{B}}_{BSpline}$$

Rearrange to solve for ${\mathbf{G}}_{BSpline}$:

$${\mathbf{G}}_{BSpline}={\mathbf{G}}_{Bezier}{\mathbf{B}}_{Bezier}{\mathbf{B}}_{BSpline}^{-1}$$

But usually, we convert from Bézier to B-Spline, so for the control points, we need:

$${\mathbf{G}}_{BSpline}={\mathbf{G}}_{Bezier}\cdot \underset{ConversionMatrix}{\underbrace{\left({\mathbf{B}}_{Bezier}{\mathbf{B}}_{BSpline}^{-1}\right)}}$$

The Conversion Matrix

$$\mathbf{M}={\mathbf{B}}_{Bezier}{\mathbf{B}}_{BSpline}^{-1}$$$$\mathbf{M}=\left(\begin{array}{cccc}6& 0& 0& 0\\ -7& 2& -1& 2\\ 2& -1& 2& -7\\ 0& 0& 0& 6\end{array}\right)$$

b)

please derive the conversion matrix to convert the control points of BSpline curve to the control points of Bezier curve.

Matrix Formulation

For both curve types:

$$Q(t)={\mathbf{G}}_{Bezier}{\mathbf{B}}_{Bezier}\mathbf{T}(t)={\mathbf{G}}_{BSpline}{\mathbf{B}}_{BSpline}\mathbf{T}(t)$$

Equating the Two Forms

For all $t$:

$${\mathbf{G}}_{Bezier}{\mathbf{B}}_{Bezier}={\mathbf{G}}_{BSpline}{\mathbf{B}}_{BSpline}$$

Solve for Bézier Control Points in Terms of B-Spline

Rearrange:

$${\mathbf{G}}_{Bezier}{\mathbf{B}}_{Bezier}={\mathbf{G}}_{BSpline}{\mathbf{B}}_{BSpline}$$

Multiply both sides by ${\mathbf{B}}_{Bezier}^{-1}$:

$${\mathbf{G}}_{Bezier}={\mathbf{G}}_{BSpline}{\mathbf{B}}_{BSpline}{\mathbf{B}}_{Bezier}^{-1}$$

Conversion Matrix (B-Spline → Bézier)

Thus, the conversion matrix is:

$${\mathbf{M}}^{\prime }={\mathbf{B}}_{BSpline}{\mathbf{B}}_{Bezier}^{-1}$$$${\mathbf{M}}^{\prime }=\left(\begin{array}{cccc}\frac{1}{6}& 0& 0& 0\\ \frac{2}{3}& \frac{2}{3}& \frac{1}{3}& \frac{1}{6}\\ \frac{1}{6}& \frac{1}{3}& \frac{2}{3}& \frac{2}{3}\\ 0& 0& 0& \frac{1}{6}\end{array}\right)$$

Question-2

Consider the cubic Bezier curve:

$$P(t)=(-1,-1{)}^T(1-t{)}^3+(1,1{)}^{T}3t(1-t{)}^2+(-1,1{)}^{T}3t^2(1-t)+(1,-1{)}^T{t}^{3}0\le t\le 1.$$

Suppose that the curve $P(t)$ is subdivided into two pieces in the middle, i.e., at $t=0.5$.
Find the control points of these two pieces, each being regarded as a cubic Bezier Curve.

Please write the pseudocode of the algorithm for finding the control points and use the line segment between the control points to draw the curve.

Let $t=0.5$.

• $P_0=(-1,-1)$

• $P_1=(1,1)$

• $P_2=(-1,1)$

• $P_3=(1,-1)$

• $1-t=0.5$

First Level ($Q$):

• $Q_0=0.5\times (-1,-1)+0.5\times (1,1)=(0,0)$
• $Q_1=0.5\times (1,1)+0.5\times (-1,1)=(0,1)$
• $Q_2=0.5\times (-1,1)+0.5\times (1,-1)=(0,0)$

Second Level ($R$):

• $R_0=0.5\times (0,0)+0.5\times (0,1)=(0,0.5)$
• $R_1=0.5\times (0,1)+0.5\times (0,0)=(0,0.5)$

Third Level ($S$):

• $S_0=0.5\times (0,0.5)+0.5\times (0,0.5)=(0,0.5)$

Final Control Points

First segment (left = $0\le t\le 0.5$):

• $P_0=(-1,-1)$
• $Q_0=(0,0)$
• $R_0=(0,0.5)$
• $S_0=(0,0.5)$

Second segment (right = $0.5\le t\le 1$):

• $S_0=(0,0.5)$
• $R_1=(0,0.5)$
• $Q_2=(0,0)$
• $P_3=(1,-1)$

---

Input:
    P0, P1, P2, P3    # Four control points of the original cubic Bézier curve
    t                 # Parameter value at which to subdivide (0 < t < 1)

Algorithm:

1. Compute first-level intermediate points:
    Q0 = (1 - t) * P0 + t * P1
    Q1 = (1 - t) * P1 + t * P2
    Q2 = (1 - t) * P2 + t * P3

2. Compute second-level intermediate points:
    R0 = (1 - t) * Q0 + t * Q1
    R1 = (1 - t) * Q1 + t * Q2

3. Compute third-level intermediate point (point on the curve at t):
    S0 = (1 - t) * R0 + t * R1

4. The two new Bézier curves will have the following control points:

    # Left segment (for 0 <= u <= t):
        Control points: [P0, Q0, R0, S0]

    # Right segment (for t <= u <= 1):
        Control points: [S0, R1, Q2, P3]

Output:
    Left segment control points:  P0, Q0, R0, S0
    Right segment control points: S0, R1, Q2, P3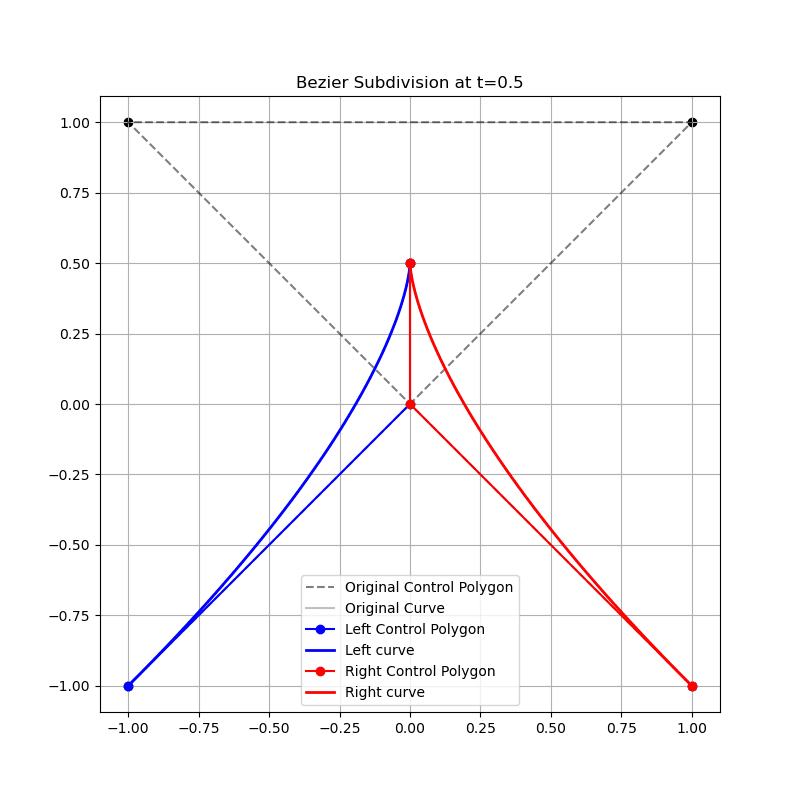

Question-3

Given two points $X_0=(-1,0{)}^T$, $X_1=(1,0{)}^T$ and two vectors $T_0=(1,1{)}^T$, $T_1=(1,-1{)}^T$, construct a cubic Bezier curve $P(t)$ such that:

• $P(0)=X_0$,
• $P(1)=X_1$,
• $P^{\prime }(0)=T_0$,
• $P^{\prime }(1)=T_1$.

Bézier Derivatives

The derivative is:

$$P^{\prime }(t)=3(1-t{)}^2(P_1-P_0)+6(1-t)t(P_2-P_1)+3t^2(P_3-P_2)$$

At $t=0$:

$$P^{\prime }(0)=3(P_1-P_0)$$

At $t=1$:

$$P^{\prime }(1)=3(P_3-P_2)$$

Set endpoints:

$$P_0=X_0=(-1,0{)}^T$$$$P_3=X_1=(1,0{)}^T$$

Tangents give:

$$P^{\prime }(0)=3(P_1-P_0)=T_0$$$$P_1=P_0+\frac{1}{3}{T}_0$$$$P^{\prime }(1)=3(P_3-P_2)=T_1$$$$P_2=P_3-\frac{1}{3}{T}_1$$

Compute $P_1$:

$$P_1=P_0+\frac{1}{3}{T}_0=\left(\begin{array}{c}-1\\ 0\end{array}\right)+\frac{1}{3}\left(\begin{array}{c}1\\ 1\end{array}\right)=\left(\begin{array}{c}\frac{-2}{3}\\ \frac{1}{3}\end{array}\right)$$

Compute $P_2$:

$$P_2=P_3-\frac{1}{3}{T}_1=\left(\begin{array}{c}1\\ 0\end{array}\right)-\frac{1}{3}\left(\begin{array}{c}1\\ -1\end{array}\right)=\left(\begin{array}{c}\frac{2}{3}\\ \frac{1}{3}\end{array}\right)$$$$P_0=\left(\begin{array}{c}-1\\ 0\end{array}\right),P_1=\left(\begin{array}{c}-2/3\\ 1/3\end{array}\right),P_2=\left(\begin{array}{c}2/3\\ 1/3\end{array}\right),P_3=\left(\begin{array}{c}1\\ 0\end{array}\right)$$

Parametric Equation

$$P(t)=(1-t{)}^3\left(\begin{array}{c}-1\\ 0\end{array}\right)+3(1-t{)}^{2}t\left(\begin{array}{c}-\frac{2}{3}\\ \frac{1}{3}\end{array}\right)+3(1-t)t^2\left(\begin{array}{c}\frac{2}{3}\\ \frac{1}{3}\end{array}\right)+t^3\left(\begin{array}{c}1\\ 0\end{array}\right)$$

Question-4

a)

Let AB and CD be two line segments in the plane with endpoints A, B and C, D, respectively. Devise an algorithm for determining if AB intersects CD.

Step 1: Bounding Box Test

• Quickly reject if the rectangles containing the two segments do not overlap. (If their x or y ranges do not overlap, the segments cannot intersect.)

Step 2: Cross Product (Straddling) Test

• Check whether the two segments “straddle” each other using the cross product:
  • If each segment’s endpoints lie on opposite sides of the other segment, or exactly on it, they intersect.

Conclusion:

• If both tests pass, the two segments intersect. If either test fails, they do not intersect.

struct Line {
    double x1, y1, x2, y2;
};

double cross(double x1, double y1, double x2, double y2) {
    return x1*y2 - y1*x2;
}

bool intersection(const Line &l1, const Line &l2) {
    if (std::max(l1.x1, l1.x2) < std::min(l2.x1, l2.x2) ||
        std::max(l1.y1, l1.y2) < std::min(l2.y1, l2.y2) ||
        std::max(l2.x1, l2.x2) < std::min(l1.x1, l1.x2) ||
        std::max(l2.y1, l2.y2) < std::min(l1.y1, l1.y2)) return false;
    double d1 = cross(l2.x2-l2.x1, l2.y2-l2.y1, l1.x1-l2.x1, l1.y1-l2.y1);
    double d2 = cross(l2.x2-l2.x1, l2.y2-l2.y1, l1.x2-l2.x1, l1.y2-l2.y1);
    double d3 = cross(l1.x2-l1.x1, l1.y2-l1.y1, l2.x1-l1.x1, l2.y1-l1.y1);
    double d4 = cross(l1.x2-l1.x1, l1.y2-l1.y1, l2.x2-l1.x1, l2.y2-l1.y1);
    if (d1 * d2 > 0 || d3 * d4 > 0) return false;
    return true;
}

b)

Let R be a four-sided convex polygon in 2D plane with vertices $P_0,P_1,P_2,P_3$. Devise an efficient algorithm for detecting whether or not a straight line l intersects the region R. Does your method still work if R is a four-sided concave polygon?

struct Point {
    double x, y;
};

int sign(double v) { 
    if (v > 0) return 1;
    if (v < 0) return -1;
    return 0;
}

// Line: Ax + By + C = 0
bool intersectsConvexQuad(Point P[4], double A, double B, double C) {
    int sgn0 = sign(A * P[0].x + B * P[0].y + C);
    for (int i = 1; i < 4; ++i) {
        int sgn = sign(A * P[i].x + B * P[i].y + C);
        if (sgn != sgn0 && sgn != 0) return true; // Opposite sides
        if (sgn == 0) return true; // Vertex on the line
    }
    return false; // All on one side
}

For Convex Quadrilaterals:

1. Substitute each of the 4 polygon vertices into the line equation (Ax + By + C = 0).
2. Record the sign of each result (positive, negative, or zero).
3. If there are both positive and negative signs (or a zero), the line crosses the quadrilateral (intersects).
4. If all signs are the same (no opposite sides), the line does not intersect the region.

The sign test method checks on which side of a line each vertex of a polygon lies. If all vertices are on the same side, it assumes the polygon and the line do not intersect.

However, this method fails for concave polygons, because:

A line can intersect a concave polygon even if all vertices lie on the same side or only one vertex lies on the line.

In concave shapes, the polygon "folds inward", so a line may pass through the interior or edges without crossing any vertex, while still cutting through the shape.

Question-5

a)

Write down the conditions for two B-spline curve segments to be position and slope continuous.

• Position continuity ($C^0$):

  • The last control point of the first segment equals the first control point of the second segment.$${\mathbf{P}}_m={\mathbf{Q}}_0$$

• Slope (tangent) continuity ($C^1$):

  • The vectors formed by the last two control points of the first segment and the first two of the second segment are equal:$${\mathbf{Q}}_1-{\mathbf{Q}}_0={\mathbf{P}}_m-{\mathbf{P}}_{m-1}$$

b)

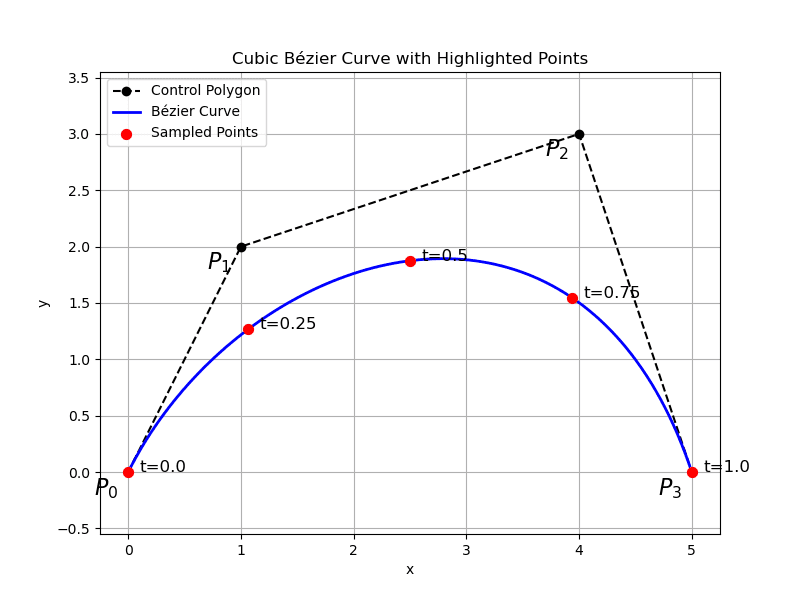
Given the control points below, plot the Bezier polynomial and highlight the points, for

$$t=0,t=\frac{1}{4},t=\frac{1}{2},t=\frac{3}{4},t=1$$

Question-6

Midpoint line algorithm for scan conversion.

The code below is an excerpt from a working version of the Bresenham midpoint algorithm for scan converting lines. You are to do the following:

a)

Write out the sequence of x,y pixel values that two calls to the bres() method would draw. The first would be with arguments 0,0,5,5 and the second call would be with arguments 1,1,5,2. Include a comment or two, in addition to just writing out the numbers.

1. First call: dobres(0, 0, 5, 5)
   • Calculate the initial decision - variable d:
     • Given x0 = 0, y0 = 0, x1 = 5, y1 = 5, we have:
       • $d=2\times (0-5)\times (0+1)+(5-0)\times (2\times 0+1)+2\times 0\times 5-2\times 5\times 0=-5$.
   • In the for - loop:
     • When x = 0, since d=-5 < 0, y is incremented to 1 and d is updated as $d=-5+2\times (5-0)+2\times (0-5)=-5$. We draw the point (0, 0).
     • When x = 1, since d=-5 < 0, y is incremented to 2 and d is updated as before. We draw the point (1, 1).
     • Repeating this process for x from 2 to 5, we get the sequence of pixel values: (0, 0), (1, 1), (2, 2), (3, 3), (4, 4), (5, 5).
2. Second call: dobres(1, 1, 5, 2)
   • Calculate the initial decision - variable d:
     • Given x0 = 1, y0 = 1, x1 = 5, y1 = 2, we have:
       • $d=2\times (1-2)\times (1+1)+(5-1)\times (2\times 1+1)+2\times 1\times 2-2\times 5\times 1=2$.
   • In the for - loop:
     • When x = 1, since d = 2>0, d is updated as $d=2+2\times (1-2)=0$. We draw the point (1, 1).
     • When x = 2, since d = 0, d is updated as $d=0+2\times (1-2)=-2$. We draw the point (2, 1).
     • When x = 3, since d=-2 < 0, y is incremented to 2 and d is updated as $d=-2+2\times (5-1)+2\times (1-2)=4$. We draw the point (3, 1).
     • When x = 4, since d = 4>0, d is updated as $d=4+2\times (1-2)=2$. We draw the point (4, 2).
     • When x = 5, we draw the point (5, 2). The sequence of pixel values is (1, 1), (2, 1), (3, 1), (4, 2), (5, 2).

b)

Compute the x,y points that would be generated for the two lines by using the standard formula y = mx + b and rounding the y values you get for each x. Do not use a calculator, since all the values will be simple fractions. Did your results agree with the values from the Bresenham algorithm? (If there's an ambiguity in rounding, go with the Bresenham value.)

1. For the line from $(0,0)$ to $(5,5)$
   • First, calculate the slope $m$ and the y - intercept $b$ using the formula $y=mx+b$.
     • The slope $m=\frac{y_1-y_0}{x_1-x_0}$, where $x_0=0,y_0=0,x_1=5,y_1=5$. So, $m=\frac{5-0}{5-0}=1$.
     • Substituting the point $(0,0)$ into $y=mx+b$, we get $0=1\times 0+b$, so $b=0$. The equation of the line is $y=x$.
     • For $x=0$, $y=1\times 0+0=0$.
     • For $x=1$, $y=1\times 1+0=1$.
     • For $x=2$, $y=1\times 2+0=2$.
     • For $x=3$, $y=1\times 3+0=3$.
     • For $x=4$, $y=1\times 4+0=4$.
     • For $x=5$, $y=1\times 5+0=5$.
     • The sequence of points is $(0,0),(1,1),(2,2),(3,3),(4,4),(5,5)$, which agrees with the result from the Bresenham's algorithm.
2. For the line from $(1,1)$ to $(5,2)$
   • Calculate the slope $m=\frac{y_1-y_0}{x_1-x_0}$, where $x_0=1,y_0=1,x_1=5,y_1=2$. So, $m=\frac{1}{4}$.
   • Substitute the point $(1,1)$ into $y=mx+b$: $1=\frac{1}{4}\times 1+b$. Then $b=1-\frac{1}{4}=\frac{3}{4}$. The equation of the line is $y=\frac{1}{4}x+\frac{3}{4}$.
     • For $x=1$, $y=\frac{1}{4}\times 1+\frac{3}{4}=1$.
     • For $x=2$, $y=\frac{1}{4}\times 2+\frac{3}{4}=\frac{2+3}{4}=\frac{5}{4}=1.25$, rounding gives $y=1$.
     • For $x=3$, $y=\frac{1}{4}\times 3+\frac{3}{4}=\frac{3+3}{4}=\frac{6}{4}=1.5$, rounding gives $y=1$.
     • For $x=4$, $y=\frac{1}{4}\times 4+\frac{3}{4}=\frac{4+3}{4}=\frac{7}{4}=1.75$, rounding gives $y=2$.
     • For $x=5$, $y=\frac{1}{4}\times 5+\frac{3}{4}=\frac{5+3}{4}=2$.
     • The sequence of points is $(1,1),(2,1),(3,1),(4,2),(5,2)$, which agrees with the result from the Bresenham's algorithm.

In both cases, the results from the standard $y=mx+b$ formula (with rounding) agree with the values from the Bresenham algorithm.

public void dobres(int x0, int y0, int x1, int y1) {
    int y = y0;
    int d = 2 * (y0 - y1) * (x0 + 1) + (x1 - x0) * (2 * y0 + 1) + 2 * x0 * y1 - 2 * x1 * y0;
    for (int x = x0; x <= x1; x++) {
        draw(x, y);
        if (d < 0) {
            y++;
            d += 2 * (x1 - x0) + 2 * (y0 - y1);
        } else {
            d += 2 * (y0 - y1);
        }
    }
} // dobres()

Question-7

Consider the program in Code A that draws a cylinder with the base lying on the x-z plane of the 3-d coordinate system (on the left of the figure). Assume that a texture of a dragon (in the middle of the figure) has been set up and texture mapping is enabled. Rewrite the program in Code B so that one complete copy of the dragon texture is mapped on the surface of the cylinder.

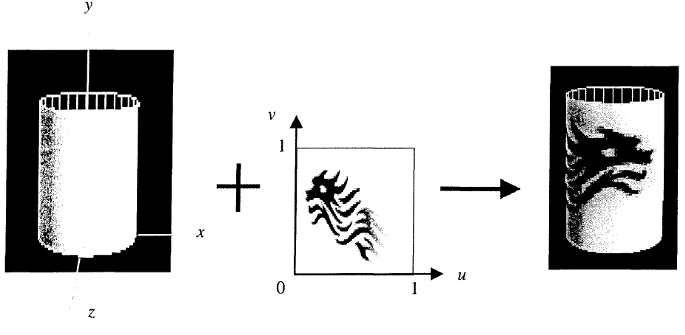
Code B:

glBegin(GL_QUAD_STRIP);
t = 0.;
dt = (360. / nslice) * 3.1416 / 180.;
for (j = 0; j <= nslice; ++j) {
    glNormal3f( cos(t), 0., sin(t));
    glTexCoord2f(j/(float)nslice, 0.0);
    glVertex3f( cos(t), 0., sin(t));
    glTexCoord2f(j/(float)nslice, 1.0);
    glVertex3f( cos(t), 2., sin(t));
    t = t + dt;
}
glEnd();